阅读:0
听报道
(1)
巴拿马运河,绵延七十七公里,连接大西洋和太平洋,从 1881年开工到1914年才真正建成。运河贯通之后,货船不必再从南美洲的霍恩角绕道,从美国西海岸到东海岸的航程缩短三分之二.
在巴拿马修建运河的想法,十六世纪就有人提出,历经各种探索和曲折,四百年后才实现.
不为多数人所知的是,虽然太平洋在大西洋的西边,但巴拿马运河在太平洋的入海口,Balboa 港口,是在运河的大西洋入海口的东南角。这条路线最短,建造费用最低.
法国人 1881年在此开工,但因高昂的工程费用和疾病死亡率,在付出近三亿美元和两万多工人的生命代价之后,被迫将工程贱卖给美国人。八十万法国投资人的资本荡然无存.
法国人转手项目之初,开价一亿美元,但是美国方面有人鼓噪从西往东横贯尼加拉瓜湖,开辟新的运河线路,以此威胁,终于将价格砍到四千万美元.
下图为在中美洲开凿运河的各种设想路线:
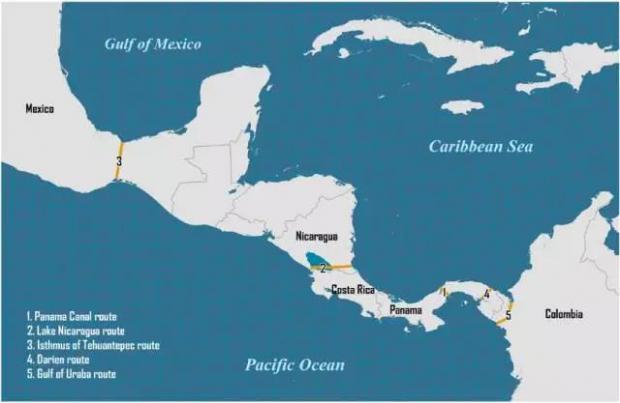
路线四,所谓 Darien route, 1698年苏格兰国王派大队人马来此勘探扎寨,但未几被西班牙人包围驱逐,苏格兰损失惨重。这也间接促成 1707年苏格兰和英格兰合并成联合王国.
路线二为直线,横贯尼加拉瓜湖,但建造工程费用过高而搁置.
路线一为巴拿马运河,从东南角向西北方向迂回. 如下图.
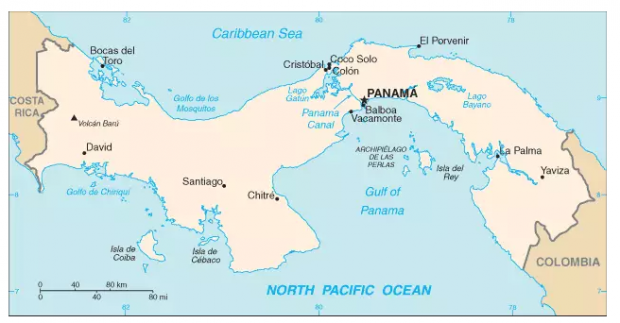
伟大的目标往往要迂回实现。 运河的最后选定路线是迂回的,即使路线确定后,工程实现中还有各种不断探索,折腾和反复.
(2)
假设你在布满迷雾的湖边,你想摸着湖底的石头到达对岸,但是迷雾让你无法对远处看得很清楚。你没有上帝视角,一眼就可以看清到达彼岸的最佳路线。你只能摸着身旁的石头,一点一点探索.
踩到一个垫脚石,你就可以看得更远一点,也许会发现新的垫脚石和路线;也许发现此路不通,然后赶快折返.
这里最大的挑战是,人们用来衡量进展的标杆,可能有很大欺骗性。如果人们仅仅以自己离对岸的物理距离来衡量进展,可能走到近前,就要达到目标时,发现前面没有垫脚石了.
美国中佛罗里达州大学计算机系教授 Kenneth Stanley 在 “伟大无法计划”一书中举了这样一个例子:
假设给你一个巨大的培养皿,让你从一个单细胞的分子开始做起,不断培养选择生物组织,让它们交配,繁衍,进化,直到制造出一个智人, 你会怎么做?
这个思想实验的本质,是看个人的判断力,是否可以做得比自然选择和适者生存更好.
按普通人的逻辑,可能就是给每个不同阶段进化出来的生物组织进行智力测验,谁智商低,就被淘汰!这样给足够长的时间,肯定进化出爱因斯坦来,不对吗?
但问题是,在通往智人进化的道路上,从单细胞,到多细胞生物,从三叶虫到两栖动物到哺乳动物,生物演化的进程中, 每一个中间步骤的垫脚石,很长时间内,其外在表现和智商,看上去没什么关系.
为了达到一个伟大的目的,我们必须对于所有的路径都保持开放的态度,即使不知道最终它将把我们带向何处.
(3)
没有有效的方向标杆, 实践上如何提高摸着石头过河的成功概率?
这里要引用一下来自材料学和统计力学里面的渗流理论 (Percolation theory).
渗流理论要解决的一个经典问题是,如果一个多孔渗水的石头,浸到水里,有多大概率中心也会湿透?
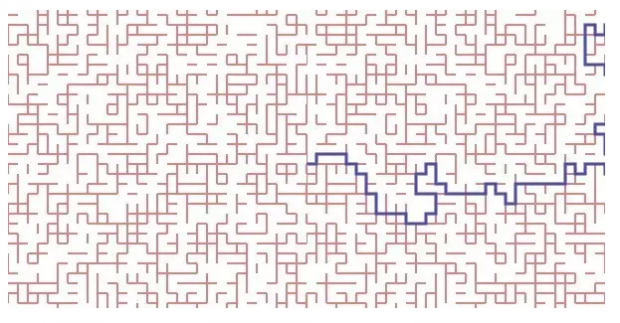
假设石头是个方形的网格,在二维空间里,每一边打开可以渗水的概率是 p. 计算结果是二维空间里 P 的临界值是 0.5, 也称渗透阈值. 对于足够大的石头,p 大于阈值时石头中心大概率是湿的。低于此阈值时则完全是干的。(如下图,纵坐标为中心渗透的概率,这里假设的是所谓 Bond Percolation 键渗透)
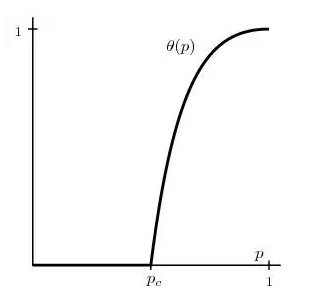
在三维空间里, P 的阈值降到 0.248.
在六维空间里,假设还是一个正方形的网格,p 的阈值 0.094, 低于 10%.
换个角度,常言 “人生不如意事,十之八九”,如意的概率还是大于 10%.
如果拓展人生的维度,达到六维,借鉴渗流理论的数学模型,给足够长的时间,在六维空间里,成功摸着石头过河,如意圆满的人生就是数学上的必然.
那么人生的维度又有哪些呢?且听下回胡侃。

话题:
0
推荐
财新博客版权声明:财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有,未经博主及/或相关权利人单独授权,任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点,不代表财新网的立场和观点。




 京公网安备 11010502034662号
京公网安备 11010502034662号 