(1)

所有没有成熟的新理论，新技术出现之初，学术界都会有两派:

好派 （人工智能，增强学习就是好, 就是好！）
    和
P 派 （人工智能，增强学习好个 P,  好个 P ! )

P 派对增强学习理论最为诟病之处：不实用，然并卵.

迄今为止关于各种算法的讨论，都离不开一个核心概念： 价值函数.

简单说，在贝尔曼方程里面，价值函数就是目前状态的理论最大值。（参见这篇老文章 王川: 深度学习有多深? (十九) -- 维度的诅咒和蒙特-卡洛模拟）

在漂亮的公式背后，如何求解价值函数，是个大问题。早期教科书里的简单例子中，价值函数就是一个表格. 每个状态，表格里对应一个函数值，在模拟和学习中不断更新.

但对于稍微复杂的问题，状态空间极大，表格根本不实用.

以围棋为例，一盘棋下完，每步棋平均有 250个选择，落棋之后平均还会走 150步，状态空间约等于 250 的150次方。 这个数字已经远超过宇宙里的原子的数目 （有估算是 10的 80次方）。计算量之大，即使用前面提到的蒙特-卡洛模拟，也无法胜任.

怎么办？解决方法是： 近似， 近似， 近似.

(2)

如何近似价值函数?

如果你还记得这篇老文章
王川: 深度学习有多深, 学了究竟有几分? (二)
86年以后，随着反向传播算法的发明，神经网络的研究开始复苏.

一些研究者，开始使用神经网络用于价值函数的近似计算.

奥地利学者 Kurt Hornik 在1991年的论文里，曾经证明，一个前馈神经网络，可以近似任何连续的非线性的函数。增加近似的精度，可以依靠增加神经元的数目实现.

神经网络用于价值函数的近似计算，它的一个优点，是相对于神经元连接的各个参数可以微分求导。通用的计算方法，是计算神经网络拟合的函数值，和实际值的方差，求导，然后使用所谓的“随机梯度下降” (Stochastic Gradient Descent) 的方法把方差最小化。

神经网络，和时间差分算法，第一个在实用上的突破，来自西洋双陆棋.

(3)

西洋双陆棋 （Backgammon)，是一个有着五千年历史的古老游戏。对弈双方各有15个棋子，每次靠掷两个骰子决定移动棋子的步数，最先把棋子全部转移到对方区域者，获胜.

1992年，IBM的研究员 Gerald Tesauro 开发了一个结合时间差分学习 （TD Learning）和神经网络的算法，给它取名 TD-Gammon,  专攻双陆棋.

 TD-gammon 使用了一个三层神经网络，如下图，棋盘状态由198个神经元代表，为输入端。中间的隐层有40-80个神经元，最后的输出值是价值函数的估算.

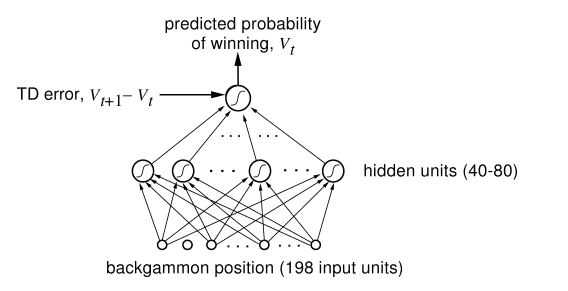
TD-gammon 最初版本，中间的隐层只有40个神经元，通过自己和自己下棋提高水平。每走一步，用时间差分算法，根据价值函数估算的差值，重新微调神经网络的参数。经过三十万个棋局的自我训练后，它达到了此前表现最好的电脑程序的水平。

此后改进版的算法，把隐层神经元数目增加到80，经过一百五十万次棋局的训练后，达到了和当时世界一流选手同等的水平.

TD-gammon 的另外一个收获是，在开局的落子上，发现了另外一种被所有前人忽略的走法，比传统走法要略优。这个新的开局走法，后被参加锦标赛的选手广泛采纳.

电脑发现了比人们的几百年，几千年来的定势思维更高明的策略, 这个现象之后将不断重复。

(4)

从 TD-gammon 算法的成功，已经隐约可以看到一个有趣的现象:

生物进化的历史, 好似算法和计算能力提高的历史.

拥有抽象的近似计算能力，只要超越对手一点点，只要进步速度比对手更快, 就可以在生存竞争中胜出，更大概率的把基因传递到下一代.

Tesauro 之后有许多研究者试图把类似 TD-gammon 的算法用到象棋，围棋和其它游戏上，但是效果并不显著。主流的看法是，因为双陆棋每个回合都要掷骰子，游戏有较大的随机性，恰好和 TD-gammon 的算法合拍. 双陆棋的成功是个特例.

增强学习从理论到计算能力上，还有太多问题要解决，差距要弥补.

"好派"阵营继续壮大，但 "P派" 底子厚，仍然不为所动.

(未完待续)