论决策机制和纠错成本
1. 每个人做决策时，势必会犯错误，严格说是偏差。这种偏差往往不是因为我们不够聪明，而是因为信息输入有局限，或者被输入了虚假的信息，更重要的是，随着时间的推移，事物的演变的复杂程度远超我们的有限思维模型可以想象的范围。所以偏差是必然，没有必要觉得丢脸或者不好意思。 2. 在必然有错误和偏差的情况下，纠错的能力就变得十分重要。但实践中根据情况变化，要做到迅速纠错，非常困难。一个重要障碍是纠错必然会...
2019年12月26日 15:27
阅读全文>>
2019年12月22日 15:18
阅读全文>>
理解别人错误观点背后的原因更重要
1. 对某一件具体的事，光知道自己的认识是正确的，别人的认识是错误的，还远远不够。我们经常看到两个人对于同一件事情有不同观点和解读，吵得脸红脖子粗，都想说服对方，甚至激烈的时候两个人要动手打起来。这是非常不值的。因为即使你知道他是错的，你如果不知道为什么原因他会有这种错误的观点，你费牛劲说服了张三，下面来了个李四还要说服他，这要把你累死。你又不是雷锋，说服这些人改变观点，对你没啥好处，可能别人还要...
2019年12月08日 13:17
阅读全文>>
下个十年 来自软件定义世界的挑战
1. 世界是个巨大的网络，在一个已经有少数垄断者的相对稳定状态的网络上，按照现有规则争夺稀缺资源，是一个极吃力而不讨好的事情。但人们被长期训练学习了现有网络上的操作规则（类似软件系统的应用程序界面 API） ，已经习惯了对于各种事情不经大脑的直觉反应 （类似电脑的缓存 cache ），从某个角度上已经成了这个操作系统上的僵尸。新的机会，只有来自网络拓扑结构的改变。 2. 网络拓扑结构的彻底改变，通常都有这样...
2019年10月05日 06:57
重要的东西往往是看不见的
（1） 俗话说， 房价的关键是，位置，位置，位置。在硅谷生活久了的人，会有一个错觉：那就是，房价总是一直涨。即使偶尔会有衰退，一般几年内就会恢复，再创新高，好区恢复得更快。房子拿出来卖，往往会有好几个买家出来抢，不断加价是常态。 前不久到东部旅行，一个朋友提到，他的房子价格仍然低于 2007年的买价， 让我吃了一惊。 硅谷很多地区的房价从 2014年之后就超过 2007年的最高点。联储局网站 stlouisf...
阅读全文>>
2019年07月29日 10:03
阅读全文>>
脑联网即将带来的智能大核爆
1. 马斯克 (Elon Musk) 旗下的脑机接口公司 Neuralink 七月十六日宣布，已经开发出一个系统，可以将三千个微型电子探针植入动物大脑，连接电子探针的芯片在实验中已经可以让猴子通过大脑控制电脑。Neuralink 计划2020年上半年开始招募志愿者，对人脑进行测试。 2. Neuralink 技术现在的程度， 也许相当于互联网早期， 1968年夏威夷大学开发的 Alohanet. 从 Alohanet 到 1993年的 Mosaic 网络浏览器的出现，等了25年；再到...
2019年06月28日 14:13
向智能合约进军的号角已吹响
1. 脸书 Libra 区块链白皮书的推出，吹响了向智能合约进军的号角。在脸书之前，区块链行业所有各类钱包软件安装总数全世界估计只有3500百万 （数据来源 statista 网站），现在这类技术将要普及到脸书平台上接近30亿用户，这是两个数量级的差别， 量变必然导致质变。 2. 白皮书里的所有约定和设想以后都是可以改的，死抠白皮书里面的字句和段落进行斩钉截铁的预测，基本是浪费时间。脸书账上有400多亿美元现金，Libra 联盟拥有...
阅读全文>>
2019年05月13日 14:42
从品牌和应用场景的思维模型看比特币
1. 笔者在“
为什么思维模型是最重要的财富（一）”一文中曾提到思维模型的重要性。 2. 搞技术的人有个误区，就是大大低估“品牌共识”的力量， 而只是一味注重简单粗暴的技术参数。 3. 举个例子，杭州西湖，有着两千多年的文化历史传承，杭州长期为历代重要经济政治中心，多少文人骚客的诗词以西湖为背景，苏轼的一句“欲把西湖比西子”， 更是把西湖的这种历史文化沉淀出的共识推到极致。但西湖实际面积不大，不到七...
阅读全文>>
2019年05月07日 12:43
阅读全文>>
Uber上市会引爆硅谷的泡沫破灭吗？
（对于未来发展的具体时间点的预测，是个非常困难的事情。笔者仍然可能在很多细节上预测错误。笔者只是在此勾画未来的多种可能性中的一种。笔者保留根据新的发展和新的信息，修正和改变观点的权利）
1/ 首先，“泡沫破灭”这个概念如何定义？
这是一个有争议的问题。但是对于硅谷的高科技公司而言，如果纳斯达克指数比最高点下跌 40%以上， 并且处于四年，甚至五年内的最低点，那么，基本上可以无可争议地说，泡沫破灭...
2019年04月07日 07:32
为什么思维模型是最重要的财富（一）
1/ 有三件事，按照重要性的排序是： 思维模型 ， 提出问题，解决问题。 2/ 思维模型的多样性和灵活性是最最重要的。如果底层思维模型都是错误的或者狭隘的，那么你上面思考和解决的问题都可能失去意义。比如说，普通人对于哈佛大学的思维模型是”某个知名大学“， 但另外一个思维模型把它看成是 ”伪装成学校的，一个享受免税待遇的大型对冲基金 ” ； 普通人把俄国看成一个欧洲大国，但有的人把它看成“一个假扮成国家的大型...
阅读全文>>
2019年03月22日 07:26
阅读全文>>
为什么宝马可能在2022年或之前破产重组
（笔者发文时不持有宝马股份，也没有做空宝马。本文表达个人观点，不构成对所述资产投资建议。投资有风险， 入市须谨慎。） 1/ 笔者最早在 2015年有文章“ 为什么传统汽车厂商大多很快会倒闭？”，曾对汽车工业的未来做过预测。2016年也发表过“ 2018，汽车工业的我靠时刻 (二)”表达了类似的观点。 2/ 德国宝马集团 2018年的年度财报刚刚出炉： 2018 vs 2017: 交付车辆增加 1.4%， 收入减少 0.8%， 税前利润下...
2019年03月01日 13:27
阅读全文>>
科幻小说连载|发散大脑（八）
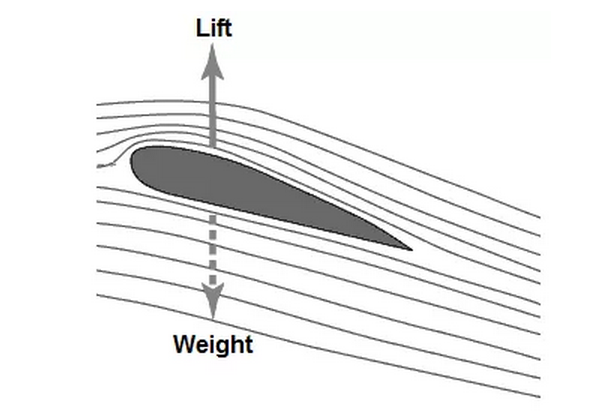
（18） “你们需要一条很长的跑道，帮助你们飞起来，飞得更高。” 巴里说道。 “跑道？ ” “飞机翅膀上的空气浮力，和飞机速度的平方成正比，这来自流体力学里的‘流线曲率定理’。 Lift = C * S * (1/2) * p * v^2 只有当空气浮力超过飞机重量时，才可以起飞。所以飞机需要一个长长的跑道，把速度给加上去。 "我当年做生意时是运气，一开始就赚钱，没有借过任何债。因为那是刚需，我几乎...
2019年01月23日 11:11
阅读全文>>
成功的关键=网络网络再网络
(1）
没经验的房地产投资者常犯的错误，是把房地产的外观和内饰等同于其价值。但是房地产其实最重要的因素是位置，位置，位置。
没经验的政客，在寻求同盟者时常犯的错误是关注其个人能力，但是政治同盟者最重要的特质是忠诚，忠诚，忠诚。如果不幸选择了能力强但不忠诚的伙伴，脑袋掉的时候还没明白是怎么回事。
专业人士常犯的错误，是埋头提升业务水平，但是事业成功的最重要因素其实是网络，网络，网络。
...
2019年01月22日 06:13
阅读全文>>
为构建多维度思维模型而值得关注的十一个人
有长期信息价值的东西一般有这几个特点： 第一，揭示了思考分析解决问题的全新的维度。 第二，通过引入新的维度，把以前看似矛盾对立的东西用统一的框架解释，并理解其各自适用的边界。 第三， 大部分人头脑僵化，对新的维度和框架有严重抵触情绪，因此多维度思考者可以对这一大批人形成较大的永久性的竞争优势。 如果一个人只被动接受社交 app 上推送的让自己爽的信息，享受那种自嗨和满足，那本质上...
2018年12月06日 12:24
阅读全文>>
王川：从算力演变看比特币现金 (BCH) 的边缘化
1/ 比特币现金 (bitcoin cash， 代码 BCH ) 是2017年八月初从比特币分叉出来的一个币。其主要动机是为了增加每个块支持的支付数目，把每十分钟出的块的大小增加到 8 MB，以降低支付费用。
2/ 比特币的主链 (btc ) 的支持者和 bch 的支持者，为区块大小的选择，吵得昏天黑地，各说各的理。
3/ btc 支付费用，因为网络拥堵，在 2017年十二月一度达到单笔要几十美元甚至更高。其中原因非常复杂。可以参见笔者的老文章
2018年12月01日 09:43
阅读全文>>
三十年前油价大跌后的最大赢家是谁？
1/ 世界历史这个复杂系统，复盘起来非常有意思。 2/ 上一次油价大跌是 1985年沙特阿拉伯大规模增产，把油价很快从 28 美元一桶打压到86年 14 美元一桶。当时沙特这样做的动机，据说主要是为了增加自己在石油输出国中的市场份额。 3/ 油价大跌的直接后果是苏联的油气出口收入大减，财政出现了高达两百亿美元的缺口，作为比较，1988年苏联的军费是八百八十亿美元。 4/ 苏联经济长期存在结构性的问题。主要表现...
2018年11月28日 13:25
阅读全文>>
2024，石油工业的我靠时刻
1/ 笔者在三年前的文章“ 为什么石油在2025年之前会永久性跌破20美元一桶，而一去不复返”，有讨论过对于油价的长期预测。现在需要重新验证一些数据。 2/ 2018年全球油耗每天九千九百万桶，中国大约一天一千三百万桶，而中国的需求在2001年时一天消耗只有四百八十万桶。 3/ 美国和欧洲的原油消耗和七十年代的水平差不多，四十年来没有增长。 4/ 毫不夸张地说，中国对原油需求的增量，是国际油价过去二十年暴...
2018年11月26日 13:06
(本文系原创科幻小说，如果人名，地名和故事情节有雷同，纯属巧合，请勿自作多情，对号入座）
(16) “你们公司现在资金状况如何？ ” 我问小驴。 “这是个好问题。我们正在和多方洽谈下一轮融资，昨天晚上的活动是宣传造势的第一步，没想到出了这个小事故。” “小驴，还记得上次苏吉特提到的巴里吗？我觉得你们应当和他争取见一面。另外，不要跟我说你们技术如何无敌，竞争者永远追不上来。重要的...
阅读全文>>
科幻小说连载：发散大脑（七）
(本文系原创科幻小说，如果人名，地名和故事情节有雷同，纯属巧合，请勿自作多情，对号入座）
(16) “你们公司现在资金状况如何？ ” 我问小驴。 “这是个好问题。我们正在和多方洽谈下一轮融资，昨天晚上的活动是宣传造势的第一步，没想到出了这个小事故。” “小驴，还记得上次苏吉特提到的巴里吗？我觉得你们应当和他争取见一面。另外，不要跟我说你们技术如何无敌，竞争者永远追不上来。重要的...
